Let’s not waste time. It’s important that I say this right from the outset.
Creativity ≠Art
Too often when we think of creativity in mathematics we jump straight to beautiful “MC Escher style” tessellations.
This “art in mathematics” is often presented as an end of term task.
It’s a little off message. You’ve been working hard on algebra or circle geometry all term, sweating over calculations and solving for x and y. You do the exam and then the teacher says, “actually maths can be art, lets look at these pretty pictures.”
Sure it’s creative but it’s hardly mathematics. And not the mathematics that we’re teaching in k-12. There’s a disconnect between what they’ve been learning and what we deem creative.
So how can we do creativity authentically in mathematics?
Earning your creativity
I remember going to a Picasso exhibition once where all his work was set out in chronological order. He spent his early years duplicating the works of others.
Picasso started his creative career at the bottom of blooms taxonomy, remembering, understanding, then applying and analysing the works of other painters.
Only once he’d worked his way through these levels could he truly start to “create”. He earned the right to be creative. So to must our mathematics students.
Before this post is done, we’ll get to creativity. But first we need to serve our artist’s apprenticeship.
An Example: Trigonometry
Stage 1. Understanding and remembering
We start at the most basic triangles. Just like young Picasso, a little bit of practise is needed here. “Boring” questions that look like this where you find x.
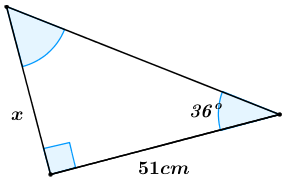Now I know, we’re talking about creativity in this post. This is where it starts. A fundamental understanding of what Trigonometry is capable of. Next you move forward a little.
Stage 2. Applying and analysing
Applications of trigonometry. Otherwise known as the dreaded “word problems”. For example:
A balloon is hovering 80m above a lake. The balloon is observed by the crew of a boat as they look upwards at an angle of 20 degrees. Twenty-five seconds later, the crew has to look at angle of 65 degrees to see the balloon. How fast was the boat traveling?
Read, interpret, draw something that looks like this, then solve.
Over many word problems students are exposed to items in the sky, Compass bearings, 3D trigonometry, reasons to find a hypotenuse, shorter side or an angle. Endless applications of this simple idea.
Stage 3. Create
Now that students know what trigonometry can (and can’t) do, they can begin to create. Not “art”, but new problems that can be solved. Let’s give them a little prompt (or boundaries) to help them along.
Task:
“Write a trigonometry word question that could take place in the fairytale land inhabited by Shrek.”
A student might reply with:
Rapunzel is in a tower 40 metres high. The tower is surrounded by a moat. Donkey and Shrek need to span the moat and save her. How long should the ladder be?
Good try, very creative. But unfortunately this is unsolveable. It resembles a trigonometry question, but it isn’t quite there. They haven’t given us enough information. If we knew how wide the moat was, then we could answer this question.
A second student might reply with:
Shrek sees Humpty Dumpty about to fall off a wall. Shrek knows he is 50 metres away from the wall and using his handy clinometer knows Humpty is at an angle of elevation of 35° . If Humpty can survive falls of up to 15 metres, Will Humpty survive this fall?
Creative? Yes. Solveable. Absolutely. This student has a very strong understanding of trigonometry. Not only can they solve routine and complex questions, they are also able to use that knowledge to create.
Apprenticeship complete. You are now the Picasso of the trigonometry world.
Where’s the authenticity?
Isn’t this all so contrived? This isn’t real world. It’s not authentic.
Good point. But in the words of Lucas from Empire Records (circa 1995)
